図1 表示システムのブロック図
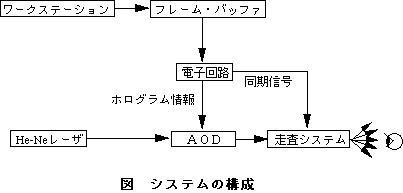
本ディスプレイシステムはホログラムの生成・伝送・表示の3つのブロックに大別 できる.図1に表示システムのブロック図の例を示す.まず,生成部ではホログラム として表示する物体の3次元データから,ホログラム上に形成される干渉縞をコンピ ュータにより計算する.その結果はフレームバッファに蓄えられてビデオ信号として 伝送される.

図1 表示システムのブロック図
表示部ではコンピュータのフレームバッファーからのCRTディスプレイ用複合映 像信号を,光学走査部分の同期信号とAODを駆動する映像(ホログラム)信号とに 分離する.
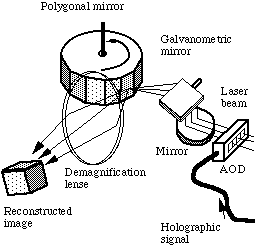
図2 表示部の光学系
図2に表示部の光学系を示す.AODの帯域に変換された電気信号がAO Dの超音波トランスデューサで超音波に変換され結晶中を伝達するとき,弾性的に変 調される屈折率変化が生じる.そのAODにレーザ光を入射すると,この屈折率変化 により光の進行方向が曲げられて出射光としてホログラム情報を持った回折光が得ら れる.AOD内に形成されたホログラムは,音速(617m/秒)で移動するため, ポリゴンミラーを音速に同期して回転することでホログラムの像を静止させる.この 同期の様子を図3に示す.

図3 干渉縞の静止と走査

図4 ポリゴンミラーの1面の大きさ
ミラーが角速度ωで回転すると,ミラーにうつったAODの像は角速度2ω で移動する.ミラーとAODとの距離をLとするとAODの像の移動速度は,2ωL である.これがAOD内の音速vと逆方向で値が等しくなればよいので,その条件は (1)式で表せる.
(1) v=2ωL
このときポリゴンミラーは同時に小さい要素ホログラムを水平走査するためにも用い られる.この水平走査によって小さいAOD結晶でも大きな再生像を得ることができ る.ミラーの一面が光を走査する時間は水平走査時間と同じである.したがって,ポ リゴンミラーの回転角速度ωとミラーの面数N,水平走査時間tHの関係は,
(2) ωN=2π/tH
となる.ポリゴンミラーの一面の幅については図4によって説明する.AODに入射 した光はΔθの範囲で回折するので,ミラーの位置での横方向へのビームの広がりはほ ぼΔθLとなる(回折角Δθは数度なのでこの近似が充分成り立つ).回折光が ミラー面の法線に対して角度φで入射すると仮定するとミラーの幅wを,
(3) w≧ΔθL/cosφ
としなければAODからの光を完全に反射させることができなくなる.ポリゴンミラ ーの一面の幅wとミラーの面数Nから,ポリゴンミラーに外接する円の半径Rは,
(4) R=w/2sin(π/N)
となる.
このような水平方向走査により形成された横長の線状ホログラムをガルバノメータ スキャナによって垂直方向に走査し,ポリゴンミラーの後に置いた出射レンズの手前 の空間に3次元像を形成する.AODの回折角はわずか3度であるため,出射レンズ によりAODの像を縮小することによって見かけ上の回折角を大きくし,広い視域を 得る.この光学系は,1930年代に研究された機械式テレビジョンである「スコフ ォニ」方式に類似しているため,「スコフォニ構成」と呼ぶこともある.
設計の一例として日本大学の表示システムを説明する.このシステムでは,画面の 毎秒更新数は60で,走査線数は33本(表示されるのは32本)で,ポリゴンミラ ーの面数は12面である.これより,水平走査時間を求めて(2)式に代入すると,ポ リゴンミラーの回転数は毎分9,600回転(=330π[rad/秒])となる. また,(1)式よりミラーとAODとの距離Lは約30cmである.ポリゴンミラーの 半径は, (4)式より4.3cm以上となる.出射レンズによる縮小倍率は4で,これ により12度の視域を得ている.
図5に日本大学の表示システムのディスプレイ部分の写真,図6に再生像(ワイヤ ーフレームによる桜の花)の例を示す.走査線数は32で,ホログラム面上の横方向 セル数は約5万である.実際の再生像は30mm×30mm×30mmで両眼視差・輻輳・焦点調 節など生理的な3次元知覚情報をすべて備えている.したがって,両眼で観察した場 合には奥行きを知覚する事ができ,視点を左右に変化させれば異なる視点からの像が 見える.3次元物体は多数の点光源の集合で表し,フレネルホログラムとして計算を おこなっている.その際,隠面処理と陰影処理を加える事で,よりリアルな再生像を 得ることもできる9).

図6 再生像の例